고정 헤더 영역
상세 컨텐츠
본문
12. 학습관련 기술들 - Optimizer
우리가 머신러닝 기초에서 배우는 SGD(확률적 경사하강법) 혹은 mini batch를 적용한 SGD는,
“비등방성 함수”( 방향에 따라 어떠한 ‘성질’이 달라지는 함수)에서의 탐색이 비효율적이다.

이 경우, 모든 좌표에 대해 기울기는 항상 중앙을 가리킨다. 즉 “기울기가 가리키는 지점”이라는 성질에 대해 “등방성”을 가진다

기울기가 가리키는 지점이 무수히 많다. 이 함수는 “기울기가 가리키는 지점” 이라는 특성에 대하여 비등방성을 가지는 함수이다.
이러한 비등방성 함수에서는 SGD Optimizer로 효율적인 탐색을 할 수 없다.

실세계의 문제들은 “비등방성”함수에서 탐색을 해야하는 경우가 대부분일 것이다.
따라서 SGD보다 더 영리한 방법들이 제시되었고, 여기에는
1. 모멘텀
2. AdaGrad
3. Adam 등이 있다.
l 먼저 SGD의 수식이다.

설명과 같이, 해당 지점에서 해당 변수로 미분한 기울기와 Learning rate(학습률)을 곱한 값을 빼주는 ( 손실함수 최소화 방향으로 ) 것이 전부이다.
l 다음은 Momentum의 수식이다.
모멘텀은 “운동량”을 뜻하는 단어로 SGD에 한가지 특성을 가미한 것이다.
운동량을 가진 것처럼, 아래 그림과 같은 작은 언덕은 쉽게 넘어갈 수 있게 ( Local Minima에 빠지지 않도록) 설계한 방식이다.

SGD에 비교하여 추가된 부분인 alpha * v 에서 alpha는 0.9와 같은 값으로 설정 ( 물리에서 마찰/저항의 역할) 갑자기 매개변수가 0이 되어 아무런 힘을 받지 않는다면 서서히 속도가 감소한다
내리막 길에 있는 경우( 편미분 값이 음수 ) : 식 6.3의 lr * 편미분 값이 음수가 되어, v값이 더 커지거나, 감소하더라도 그 폭이 작아진다. 해당 변수가 커지려는 “힘”이 증가한다.
오르막 길에 있는 경우: 식 6.3의 lr*편미분 값이 양수가 되어 v의 감소폭이 커진다. 즉, 변수 W가 작아지려는 “힘”이 증가한다

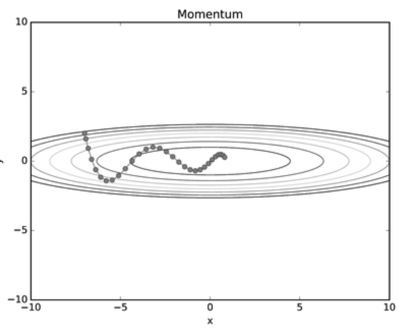
위와 같이 Momentum이 더 안정적으로 수렴하는 것을 확인할 수 있었다.
Momentum방식의 더 큰 장점은 Local Minima에 빠지는 경우를 SGD에 비해 많이 해결해준다는 것이다.
l 다음은 AdaGrad방식이다.

학습을 진행하며, Learning Rate를 점차 줄여가는 방법!
매개변수 전체의 Learning Rate를 일괄적으로 낮추기보다, “각각의” 매개변수에 “맞춤형”값
l h값에 기존 편미분(기울기)값을 제곱하여 더해준다. (Element wise Multiply)
l 즉, 학습이 진행될수록, h값은 계속 커지고, 많이 움직인 매개변수는 학습률이 점점 낮아지게 된다 ( W값 갱신시, LearningRate 옆에 sqrt(h)로 나누어 주므로 )
학습을 진행할수록 갱신 강도가 약해져, 어느 순간 갱신량이 0이 되어 전혀 학습이 이루어지지 않는 상황이 오며, 이를 개선한 RMSProp라는 방식이 제안되었다.
l 다음은 Adam Optimizer이다.
모멘텀 + AdaGrad 융합한 듯한 방식.
l 매개변수 공간을 효율적으로 탐색
l Hyper Parameter의 “편향보정”이 진행됨
l 3개의 Hyper Parameter를 설정
1. 지금까지의 학습률 alpha
2. 일차 모멘텀용 계수 Beta1 = 0.9
3. 이차 모멘텀용 계수 Beta2 = 0.999
Optimizer는 해결해야할 문제에 따라 다르게 선택해야한다.
Ø MNIST 데이터셋에 대하여 4가지 Optimizer를 적용해본 결과

**Optimizer와 신경망의 구조 뿐 아니라, 학습률, 가중치의 초기값에 따라서도 학습의 결과가 크게 달라진다.
'ML&DL' 카테고리의 다른 글
| MLDL 학부연구생 학습내용 정리03 - 가중치의 초기값 (0) | 2022.10.10 |
|---|---|
| 학부연구생 딥러닝 기본개념 학습내용 복습-01 순전파와 역전파&활성함수 (0) | 2022.10.09 |
| Hyperparameter 종류와 Tuning (0) | 2022.10.06 |
| SGD와 Weight Decay regularization (0) | 2022.10.06 |
| Sigmoid함수와 Gradient Descent를 위한 cross-entropy 미분 (0) | 2022.10.03 |




