고정 헤더 영역
상세 컨텐츠
본문
# Softmax (Normalized Exponential - 모든 값이 0~1사이 값이 되므로)함수 :
Softmax 함수는 "출력층"에서 사용되는 함수이다.
모든 입력신호로부터 영향을 받는다. 이는 "확률적 해석"을 가능하게 하려는 설계 목적 때문.
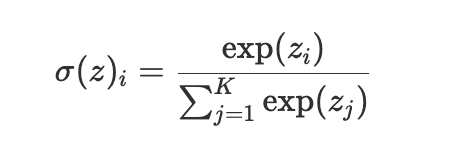
K: 클래스 수 , Zj는 Softmax 함수의 입력값
# 지수함수 사용으로 얻는 점 :
- 1. 큰 값은 더 크게, 작은 값은 더 작게
- 2. 미분 가능해짐
# Layer 은닉층에서 사용할 수 는 없는가? :
- 1. 없다. 애초에 출력층에서 사용하기 위해 설계된 함수이며, 중간층에서 사용할 경우, 정보 손실이 일어난다.
# Softmax함수 주의점 :
- 1. 지수함수이므로 OVerflow 문제가 발생할 수 있다.
- 2. 아래와 같이 분모, 분자에 같은 수를 곱하여 지수로 올려주어 지수함수를 컨트롤해준다.
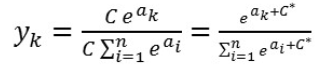
# Softmax함수 특징 :
- 1. 출력 값이 0~1 사이 실수이며, 총합은 1 => 확률적으로 해석할 수 있다.
- 2. Softmax
# Softmax함수 미분 :
- 1. 해당 입력변수에 대하여 미분 한 경우
- 2. 다른 입력변수에 대하여 미분한 경우

# Softmax함수를 사용할 때의 Loss함수(다중 Cross-entropy)의 형태와 미분 :

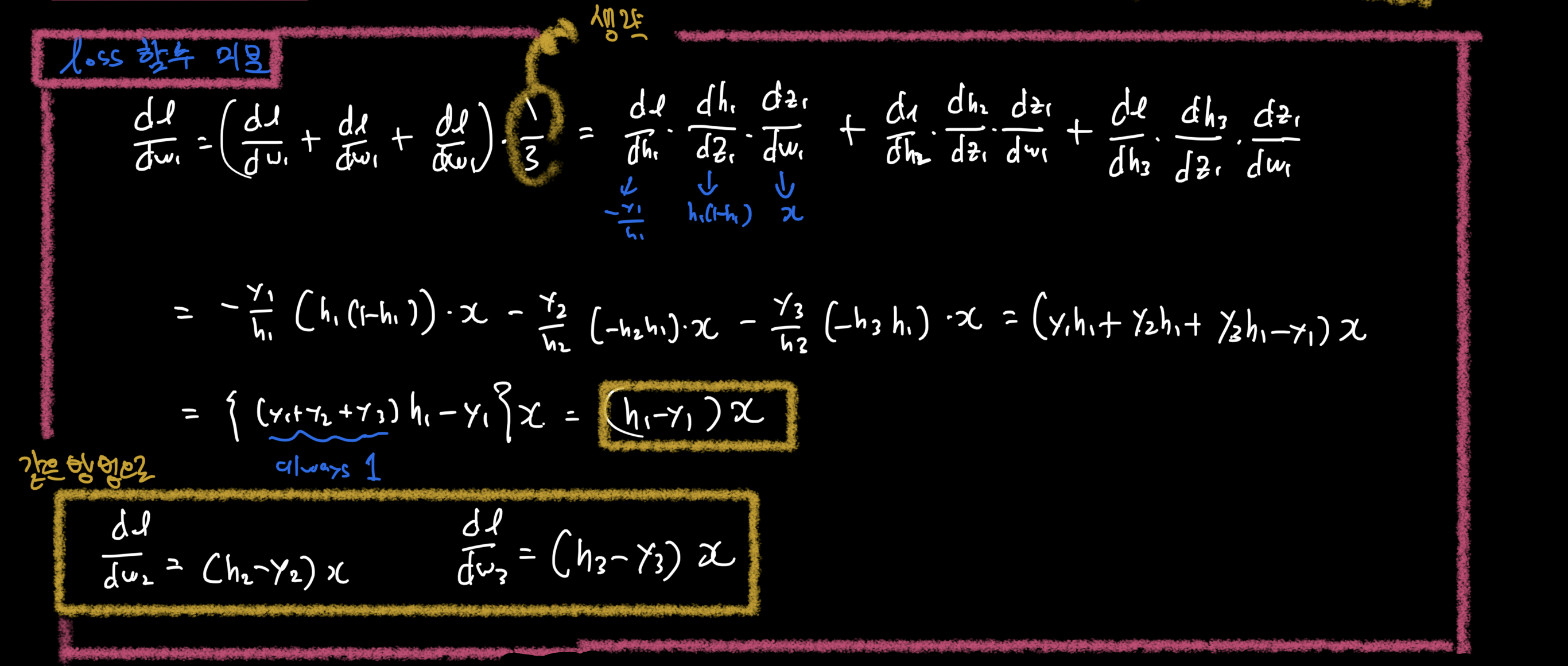
<코드>
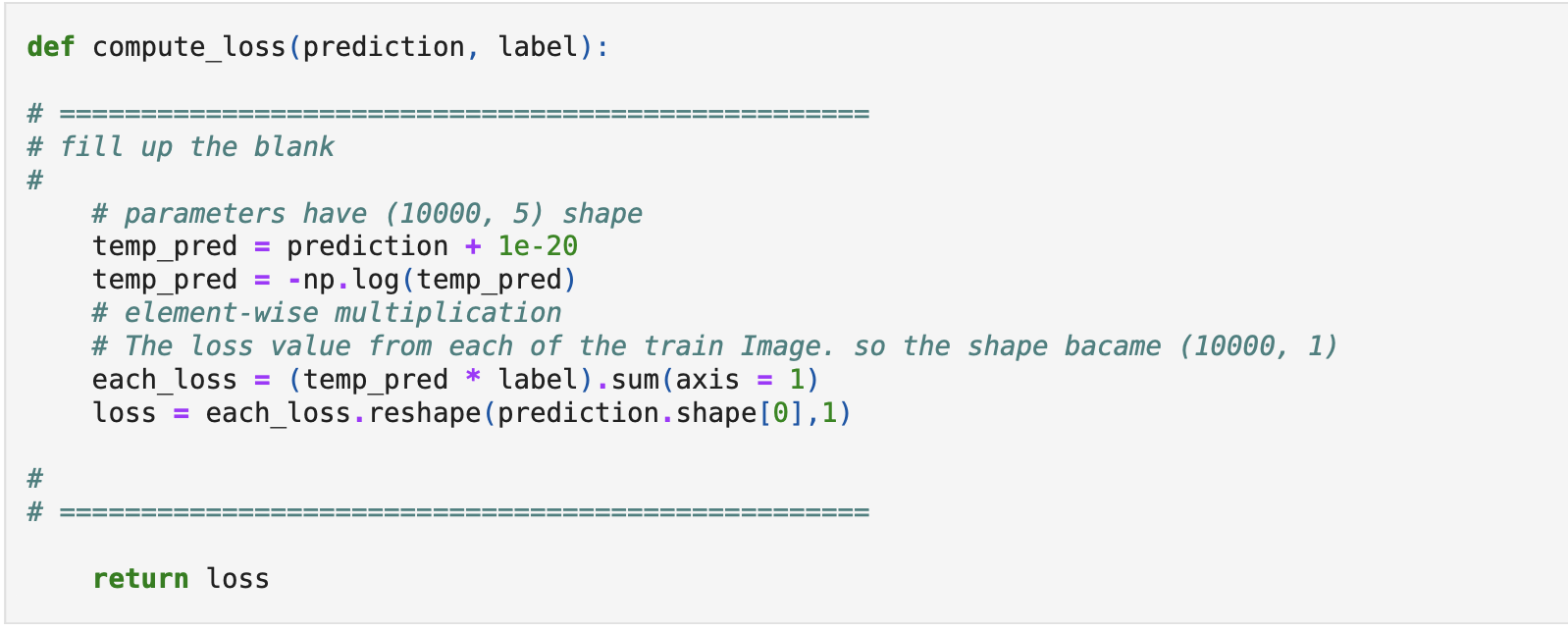
우리가 정의한 loss함수는 다중 cross-entropy였으므로, 자연로그를 사용해야했다.
# 로그에 0을 넣어주면 nan이 되기 때문에, 이를 방지하기 위해 1e-20이라는 아주 작은 값을 모든 element에 더해줬다.
각 행의 모든 값들을 더하여, 최종적으로 각 행이 나타내는 것은 각 input case의 loss값이 된다.

딥러닝분야에서 batch_size라는 단어를 많이 들어보았을 것이다.
신경망이 학습할 때, train data를 하나씩 넣지 않는다. 여러개의 data를 함께 넣어 빠르게 연산을 하게 되는데,
코드를 작성할 때, 각 행렬의 행/열이 어떤 것을 의미하고, 어떤 형태고 dot연산을 해줘야 의미상으로 적절한지 생각해보는 것이 쉬운 일은 아니다.
우리가 정의한 weight에 대한 gradient descent 공식은 아래와 같았고,
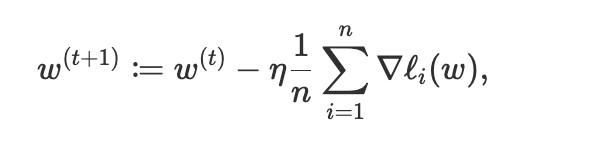
여기서 정의한 loss함수에 대한 gradient는 아래와 같았다.

따라서 prediction ( 10000개 data수, 5_class수) shape을 가진 prediction(softmax를 거쳐 나온 추론값)과 label(ground truth)를 빼주어, (10000, 5)shape의 array를 만들어야겠다는 생각을 하는 것은 어렵지 않을 것이다.
이후에 , x 즉, input data와 곱셈(element-wise)을 통해 weight와 같은 shape의 array를 도출해내야하는데, ( weight는 (784,5)의 shape를 가지고 있었다. )
input을 transpose하여 dot product를 해야할 것 같은데, 이를 완벽히 머리로 이해하는 것이 쉽지 않았다.
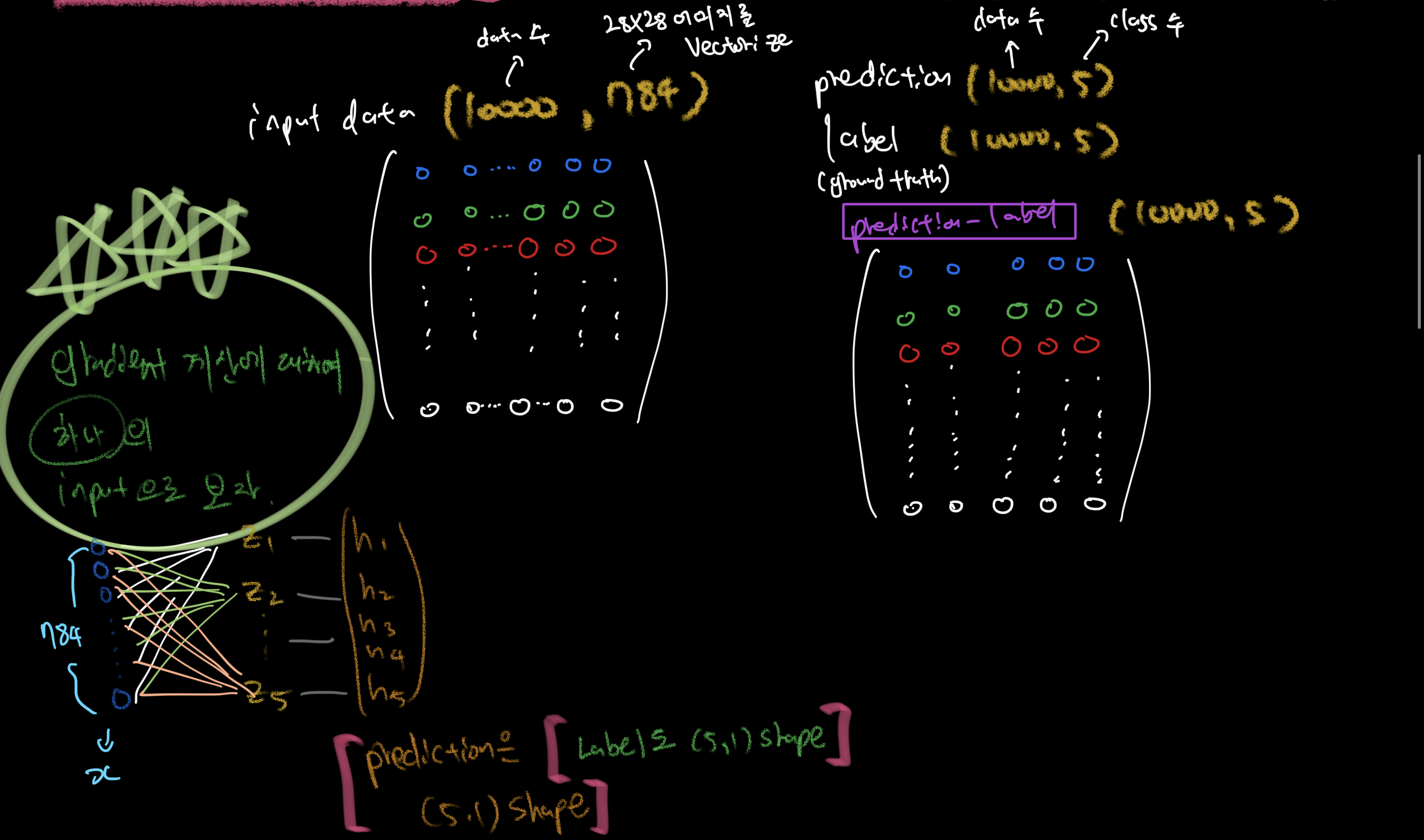



위와 같은 논리로 해당 과제와 같은 batch학습( 모든 데이터를 한 번에 다 연산하고 weight갱신)에서 gradient 구하는 코드를 아래와 같이 작성하였다!

'ML&DL' 카테고리의 다른 글
| 학부연구생 딥러닝 기본개념 학습내용 복습02 - Optimizer (0) | 2022.10.09 |
|---|---|
| 학부연구생 딥러닝 기본개념 학습내용 복습-01 순전파와 역전파&활성함수 (0) | 2022.10.09 |
| Hyperparameter 종류와 Tuning (0) | 2022.10.06 |
| SGD와 Weight Decay regularization (0) | 2022.10.06 |
| Sigmoid함수와 Gradient Descent를 위한 cross-entropy 미분 (0) | 2022.10.03 |




